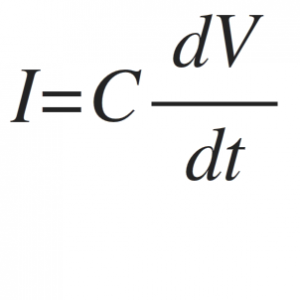In the previous sections we saw that the building blocks of capacitor are the parallel metallic pates on which the Positive and negative electric charges are developed. These metallic plates are separated by the dielectric material so that the two metallic plates should not to touch each other. Further, in this kind of capacitor when we apply the DC potential then the the charging current is flowing through the capacitor due to which the electric charges are developed at one of the plate of the capacitor. And equal amount of image charges are developed at the other plate. Due to the electric charges are stored in the capacitor. The charge stored in the capacitor is Q which is measured in Coulomb. Thus, the amount of charge stored in the capacitor is depends upon the applied potential difference.
The most important parameter involved in the capacitor is the capacity to store the charge between two metallic plates which is nothing but the capacitance of the capacitor.
Thus the charge stored in the capacitor s directly proportional to the applied voltage between the two plates.
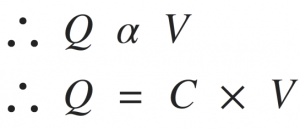
Where C is the constant of proportionality known as capacitance and measured in Farads.
Q is the stored electric charge in Coulombs and V is the applied electric potential in V.
From the above equation it can be seen that, if we increase the applied potential the charge stored in the capacitor increases linearly. Hence, lower is the applied voltage lower is the charge stored in the capacitor. Higher is the applied potential, larger is the charge stored in the capacitor.
Hence the equation which indicates that, the charge stored in the capacitor directly proportional to the applied electric potential can be represented in three forms as shown below,

Thus, one Farad capacitance is the ability of capacitor to store the charge of one Coulomb at an applied voltage of one Volt between the plates. Thus in the capacitor equation three scientists names are involved that are, Michael Faraday, Charles-Augustin de Coulomb and Italian physicist Alessandro Volta. Thus from the capacitor equation it can be seen that, larger the value of the capacitance, larger is the electric charge storage in the capacitor.
The capacitance value depends upon the dimensions of the capacitor structure. The parameters involved are,
The cross-section area of the capacitor, i.e. A in meter^2
The distance between the two plates, i.e. d in meter
The dielectric constant of the material εr
The capacitor equation in the form of this parameters is given by,
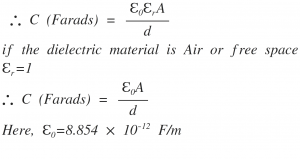
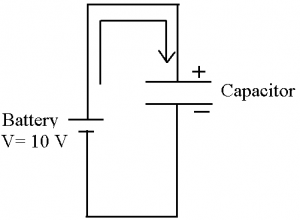
Charging of Capacitor:
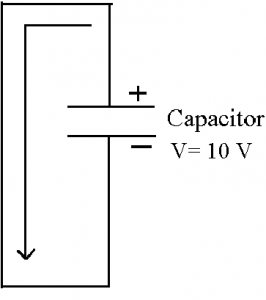
In the circuit below, by the application of the battery potential the capacitor will be fully charged upto the voltage of 10 V. This is because of the charging current flowing through the circuit. When the capacitor is fully charged then the charging current of the circuit stops flowing through the circuit. In this case the voltage stored in the capacitor is 10 V. The taken by the capacitor to charge at fully charge position is called as charging time of the capacitor
Discharging of Capacitor:
When the capacitor is fully charged then the capacitor is acts as 10 V battery source. When the two terminals of the capacitor are shorted together then the capacitor starts discharging. The time taken by the capacitor to discharge is called as the discharging time. Circuit below shows the discharging circuit of the capacitor.
As we know that, the current is related to the electric charge. The relation between the curren and charge is given by,
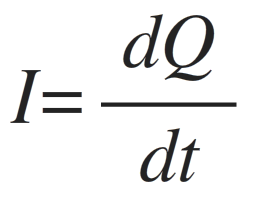
From the charge, capacitance and voltage equations we know that,
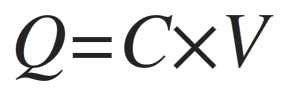
By substituting the equation of charge in the current equation we get,
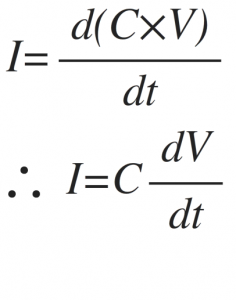
Thus, the charging current of the capacitor is given by,