Statement of the Norton's theorem :
Any linear network containing of active sources and bilateral elements can be replaced by an equivalent circuit containing a current source called Nortons equivalent current (IN or ISC) and an equivalent impedance in parallel (ZTH or Zeq) across the two terminals of the load. IN is the short circuit current flowing through the short circuited path that is replaced instead of load impedance ZL. Hence it is also called short circuit current ISCor Nortons current IN. The equivalent impedance Zth is obtained when looking through load impedance, with load impedance ZL removed and all the independent voltage/current sources are replaced by their internal impedances.
It was demonstrated that every voltage source with a series internal resistance has a current source equivalent. The current source equivalent of the Thévenin network, can be determined by Norton's theorem.
The theorem states the following:
Any two-terminal linear bilateral dc network can be replaced by an equivalent circuit consisting of a current source and a parallel resistor, as shown in Figure. The discussion of Thévenin's theorem with respect to the equivalent circuit can also be applied to the Norton equivalent circuit. The steps leading to the proper values of IN and RN are now listed.
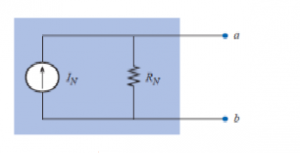
Preliminary:
1. Remove that portion of the network across which the Norton equivalent circuit is found.
2. Mark the terminals of the remaining two-terminal network.
RN:
3. Calculate RN by first setting all sources to zero (voltage sources are replaced with short circuits, and current sources with open circuits) and then finding the resultant resistance between the two marked terminals. (If the internal resistance of the voltage and/or current sources is included in the original network, it must remain when the sources are set to zero.) Since RN = RTh, the procedure and value obtained using the approach described for
Thévenin's theorem will determine the proper value of RN.
4. Calculate IN by first returning all sources to their original position and then finding the short-circuit current between the marked terminals. It is the same current that would be measured by an ammeter placed between the marked terminals.
5. Draw the Norton equivalent circuit with the portion of the circuit previously removed replaced between the terminals of the equivalent circuit.
Steps to be followed to apply the Norton's Theorem :
Step 1 : Short circuit the required branch and calculate the short circuit current ISC by using Kirchhoff's laws.
Step 2 : Calculate ZTH (Thevenin's equivalent impedance) for the circuit.
Step 3 : Draw the Norton's equivalent circuit and calculate the current through the required branch as,