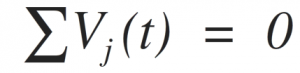Kirchhoff’s voltage law is also called as Mesh or Loop law. The Kirchhoff’s voltage law (KVL) states that the algebraic sum of the voltage around a closed loop in a circuit must be equal to zero. This is mathematically expressed as,
The other statement of KVL is that, the sum of the voltage rises is equal to the sum of the voltage drops around a closed loop in a circuit.
Further, Kirchhoff's voltage law (KVL) can also be stated as the algebraic sum of voltages around any closed path in a circuit is zero. This is mathematically expressed as,
Where Vj (t) is the voltage across the jth branch (with proper reference direction) in a loop containing N voltages.
In Kirchhoff's voltage law, the algebraic sign is used to keep track of the voltage polarity. In other words, as we traverse the circuit, it is necessary to sum the increases and decreases in voltages to zero. Therefore, it is important to keep track of whether the voltage is increasing or decreasing as we go through each element. We will adopt a policy of considering the increase in voltage as negative and a decrease in voltage as positive.
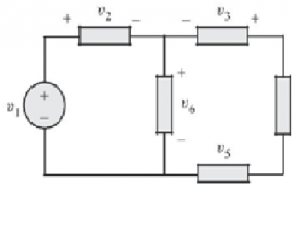
Consider the circuit shown in above figure, where the voltage for each element is identified with its sign. The ideal wire used for connecting the components has zero resistance, and thus the voltage across it is equal to zero. The sum of voltages around the loop incorporating is,
The sum of voltages around a loop is equal to zero. A circuit loop is a conservative system, meaning that the work required to move a unit charge around any loop is zero. However, it is important to note that not all electrical systems are conservative. Example of a non-conservative system is a radio wave broadcasting system.