Home > Analog CMOS Design > CMOS Differential Amplifier > Differential Amplifier

The important advantage of differential operation over single ended operation is higher immunity to noise. The simple differential amplifier is as shown in Figure below.

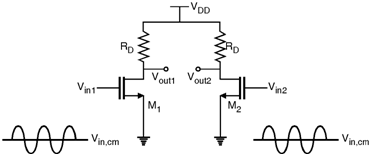
The other advantage of differential amplifier is the increase in voltage swings. The peak to peak swing differential amplifier is equal to 2 [V _DD - (V_GS - V_TH)].

In the circuit of above Figure if V_in1 and V_in2 has a large common mode disturbances or unequal common mode dc level then the output response has distortions. As V_{in, cm} changes, bias currents of M₁ and M₂ also changes. Thus the transconductance of both the devices and output common mode dc level changes. The variation of the transconductance in turns leads to change in the small signal gain of the amplifier.

In order to solve the problem of common mode dc level the circuit shown in above figure is modified by employing a current source I_SS to make (I_D1 + I_D2) independent of V_{in, cm}.

The modified circuit incorporating current source I_SS is as shown in Figure below.

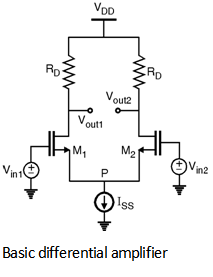
Thus, if V_in1 = V_in2 the biasing current of each transistor equals and the output common mode level is V_DD - .

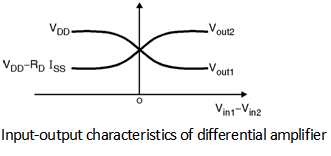
The input-output characteristics differential pair is as shown in Figure below.

In order to derive the voltage gain of the differential amplifier. Let us consider the circuit of basic differential amplifier

From Figure it is found that,

V_GS1 = V_in1 - V_P and V_GS2 = V _in2 - V_P

\ V_in1 - V_GS1 = V_in2 - V_GS2

i.e. V_in1 - V_in2 = V_GS1 - V_GS2

Now, according to saturation current equation of MOSFET.

(V_GS - V_TH)² =

\ V_GS = + V_TH

\ V_GS1 = + V_TH

and V_GS2 = + V_TH

Assuming equal dimensions of two transistors we get,

V_GS1 - V_GS2 = -

\ V_in1 - V_in2 = -

Take square on both sides.

(V_in1 - V_in2)² = - +

(V_in1 - V_in2)² = (I_SS - 2 ) [ I _D1 + I_D2 = I_SS]

i.e.

m_n C_ox (V_in1 - V_in2) ² - I_SS = - 2

Squaring on both sides,

(V_in1 - V_in2)⁴ - I_SS m_n C_ox (V_in1 - V_in2)² + I_SS² = 4 I_D1 × I _D2

But,

4 I_D1 × I_D2 = (I_D1 + I _D2)² - (I_D1 – I_D2)²

= I_SS² - (I_D1 - I_D2) ²

By using this in the equation,

We get, (I_D1 - I_D2)² = - (V_in1 - V_in2)⁴ + I_SS m_n C _ox (V_in1 - V_in2)²

\ I_D1 - I_D2 = m_n C_ox (V_in1 - V_in2)

Thus, if V_in1 = V_in2 then I_D1 - I_D2 falls to zero, and increases from zero if | V_in1 - V_in2 | increases.

If I_D1 - I_D2 = D I_D and V _in1 - V_in2 = D V_in

\ = m_n C_ox

For D V_in = 0, The overall transconductance

G_m =

Hence, V_out1 - V_out2 = R_D (I_D1 - I_D2)

= R_D × G_m D V_in

\ = × R_D

\ | A_n | = × R_D

For a fully symmetric differential pair which senses inputs by equal and opposite amounts then the concept of half circuit can be applied to find the gain of the differential amplifier.

For the circuit shown in below Figure, by using the concept of half circuit, the small signal gain is given as,

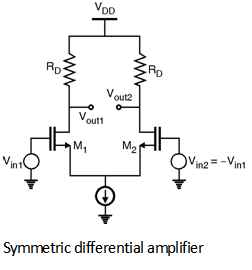
V_out1 = - g_m (R_D || ro) V_in1

V_out2 = - g_m (R_D || ro) (- V_in1 )

V_out1 - V_out2 = - g_m (R_D || ro) V_in1 - g_m (R_D || ro) V_in1

i.e. = - g_m (R_D || ro)

\ A_n = - g_m (R_D || ro)

Also, If V_in2 ¹ - V_in1 then using Half circuit concepts,

V_out1 = - g_m (R_D || ro) V_in1, V _out2 = - g_m (R_D || ro) V_in2

V_out1 - V_out2 = - g_m (R_D || ro) (V_in1 - V_in2)

\ = - g_m (R_D || ro)

\ A_n = - g_m (R_D || ro)

Differential Pair with Current Source Loads :

In order to increase the gain of the amplifier the load resistance can be replaced by the current source load as shown in Figure below.

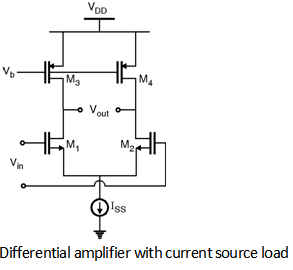
By using half circuit concept the gain can be given as :

A_n = - g_{m1, 2} (ro_{1, 2} || ro_{3, 4} )