Statement of the superposition theorem :
The superposition theorem states that in any linear network containing two or more sources, the response (current) in any element is equal to the algebraic sum of the response (current) caused by individual sources acting alone, while the other sources are inoperative.
In any linear bilateral network containing two or more independent sources (voltage or current sources or combination of voltage and current sources ), the resultant current voltage in any branch is the algebraic sum of currents / voltages caused by each independent sources acting along, with all other independent sources being replaced meanwhile by their respective internal resistances.
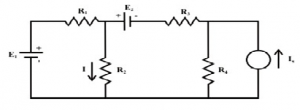
Superposition theorem can be explained through a simple resistive network as shown in figure and it has two independent practical voltage sources and one practical current source.
One may consider the resistances R1 and R3 are the internal resistances of the voltage sources whereas the resistance R4 is considered as internal resistance of the current source. The problem is to determine the response I in the in the resistor R2. The current I can be obtained from,
Where I= total current
= current due to E1 source
= current due to E2 source
= current due to Is source
according to the application of the superposition theorem. It may be noted that each independent source is considered at a time while all other sources are turned off or killed. To kill a voltage source means the voltage source is replaced by its internal resistance whereas to kill a current source means to replace the current source by its internal resistance.
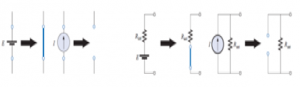
To consider the effects of each source independently requires that sources be removed and replaced without affecting the final result. To remove a voltage source when applying this theorem, the difference in potential between the terminals of the voltage source must be set to zero (short circuit); removing a current source requires that its terminals be opened (open circuit). Any internal resistance or conductance associated with the displaced sources is not eliminated but must still be considered. Figure reviews the various substitutions required when removing an ideal source and Figure reviews the substitutions with practical sources that have an internal resistance.
The total current through any portion of the network is equal to the algebraic sum of the currents produced independently by each source. That is, for a two-source network, if the current produced by one source is in one direction, while that produced by the other is in the opposite direction through the same resistor, the resulting current is the difference of the two and has the direction of the larger. If the individual currents are in the same direction, the resulting current is the sum of two in the direction of either current. This rule holds true for the voltage across a portion of a network as determined by polarities, and it can be extended to networks with any number of sources. The superposition principle is not applicable to power effects since the power loss in a resistor varies as the square (nonlinear) of the current or voltage.
Steps to be followed to apply the superposition theorem :
Step 1:Select any one energy source.
Step 2:Replace all the other energy sources by : their internal series resistances for voltage sources. their internal shunt resistances for current sources.
Step 3:With only one energy source calculate the voltage drops or branch currents paying attention to the voltage polarities and current directions.
Step 4:Repeat steps 1, 2 and 3 for each source individually.
Step 5:Add algebraically the voltage drops or branch currents obtained due to the individual source to obtain the combined effect of all the sources.
Limitations of superposition Theorem
Superposition theorem doesn't work for power calculation. Because power calculations involve either the product of voltage and current, the square of current or the square of the voltage, they are not linear operations. Superposition theorem can not be applied for non linear circuit ( Diodes or Transistors ).
This method has weaknesses:- In order to calculate load current I or the load voltage V for the several choices of load resistance R of the resistive network , one needs to solve for every source voltage and current, perhaps several times. With the simple circuit, this is fairly easy but in a large circuit this method becomes an painful experience.
Questions
- What kinds of circuits can be solved by superposition?
- What are the steps to solve a circuit using the superposition theorem?
- How are different kinds of sources treated when solving by superposition?
- How do I use superposition to solve a circuit?