Home > Analog CMOS Design > MOSFET Parasitics > Parasitic capacitance Models

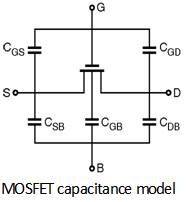
In integrated circuits the capacitances associated with the devices are taken into account to understand the behaviour of the circuits. For this purpose a model of capacitances is needed. The various capacitances associated with the MOSFET are shown in Figure below. The various capacitance involved are,

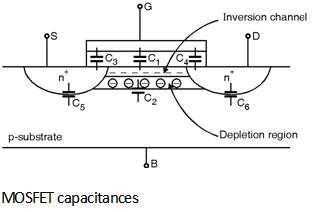
C₁ Þ gate Oxide capacitance

C₂ Þ Depletion capacitance

C₃ Þ Overlap Capacitance between gate poly and the source

C₄ Þ Overlap Capacitance between gate poly and the drain

C₅ Þ Junction capacitance between source and the substrate

C₆ Þ Junction capacitance between drain and the substrate

Gate Capacitance Model :

The gate capacitance (C_g) is decomposed into two elements each with different behaviour, one part of C_g contributes to the channel charge and another part is due to the MOS structure.

Channel Charge Capacitance :

The channel charge capacitance is derived from the gate to channel capacitance C_GC which consists of, 1) gate to source (C_GCS), 2) gate to drain (C_GCD), and 3) gate to Body (C _GCB) capacitances. These capacitances are depend upon the operation region and terminal voltages. When the transistor is in the cut-off region no channel exists and C_GC appears between gate and body.

In the linear region an inversion layer is formed which acts as a conductor between source and drain. Hence C_GCB = 0 as the body electrode is shielded from the gate by the channel and by using the symmetry the total capacitance C_GC is distributed evenly between source and drain.

In the saturation mode the channel is pinched off hence the capacitance between gate and drain is C_GCD = 0 as well as the capacitance between gate and body i.e. C_GCB = 0 therefore the total capacitance C_GC is represented by the gate to source capacitance C_GCS.

The actual value of the total Gate to channel capacitance (C_GC) its distribution over three components (C_GCB, C_GCS and C_GCD) is given as below :

For V_GS = 0 the transistor is OFF no channel is present and the total capacitance appears between gate and body which is given as :

C_GC = C_ox × W × L

When we increase V_GS a depletion region forms under the gate this appears as an increase in the thickness of the gate dielectric which results in a reduction in capacitance. Which was shown in C-V characteristics in Fig. 8.6.4 once the transistor turns ON (V_GS = V_TH) a channel is formed and C_GCB drops to '0' with V_DS = 0 the devices operates in the linear mode and the total capacitance is divided equally between source and drain which is given as :

C_GCS = C_GCD =

Once the transistor is ON the distribution of its gate capacitance depends upon the degree of saturation measured by the ratio .

In the saturation mode C_GCD gradually drops to '0' for increasing the levels of saturation while C_GCS increases. Hence the total gate to channel capacitance is represented by C_GCS which is given as :

C_GCS = C_ox × W × L

MOS Structure Capacitances :

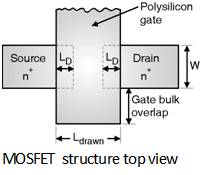
Consider the structure of MOS transistor shown in Figure below. Ideally the source and drain diffusion should end right at the edge of the gate oxide.

But in reality both source and drain tend to extend some what below the oxide by an amount L_D called as lateral diffusion. Hence the effective channel length of the transistor becomes shorter than the drawn length L_drawn by a factor 2 L_D. This gives rise to a parasitic capacitance between gate and source as well as gate and drain this type of capacitance is called as the overlap capacitance. This capacitance is given as :

C_gso = C_ox × L_D × W and C_gdo = C_ox × L_D × W

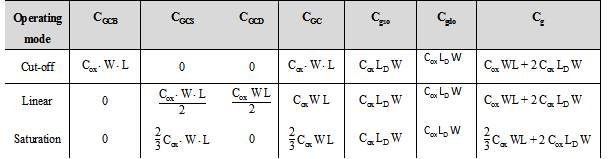
The average distribution of all the gate capacitance in cut-off, linear and saturation region of operation is given in Table below.

Diffusion Capacitance Model :

The diffusion capacitance also called as junction capacitance is contributed by the reverse biased source-body and drain-body pn junctions. This type of junction capacitance is non linear and decreases when the reverse bias is increased.

The components of diffusion capacitance at source or drain region are shown in
Figure below. The diffusion capacitance also includes the capacitances due to bottom plate junction and side wall junctions.

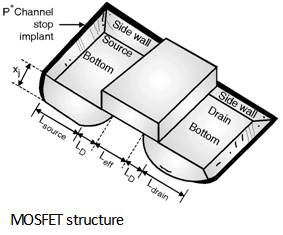
The bottom plate junction is formed between source and the substrate. This capacitance is given by,

C_bottom = C_j W × L_source

Where C_j is the junction capacitance per unit area.

Further, the side wall junction is formed by source and channel stop implant This capacitance is expressed as,

C_sw = C_jsw ´ (W + 2 L_source)

Thus, Total diffusion capacitance for source is expressed as,

C_diff = C_bottom + C_sw = C_j ´ Area + C_jsw ´ Perimeter

= C_j L_source W + C_jsw (W + 2 L _source)

Further, the total diffusion capacitance for drain side is expressed as, :

C_diff = C_j L_drain W + C_jsw (W + 2 L_drain)

Capacitance Device Model of MOSFET :

All the contributions of capacitances can be combined in a single model for the MOS transistor as shown in Figure below.The equation which relates all the capacitances is given as :

C_GS = C_GCS + G_GSO ;

C_GD = C_GCD + C_GDO ;

C_GB = C_GCB

C_SB = C_{S diff}

C_DB = C_{D diff}

Thus for designing high performance and low energy circuits to this model is strongly required.