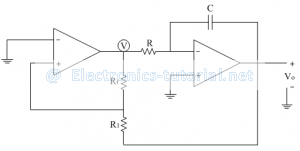
Comparator can be used as a function generator. It is basically an oscillator circuit.(i.e. it doesn't have any external input). Such a function generator using op-amp is shown below which generates triangular and square waveforms.
The first op-amp is non-inverting type of Schmitt trigger. Inverting terminal is grounded so Vref = 0V.
The output of first op-amp is voltage V, which is basically a square wave. This output is connected to an ideal integrator. The feedback path is completed as shown in the circuit diagram which defines the magnitude of output triangular wave.
The output of the Schmitt trigger is either +Vsat or –Vsat. The circuit is explained by drawing waveforms at different points.
For a non-inverting Schmitt trigger, the threshold point is given as
±VT=±R1/Rf (Vsat )
Let Rf=KR1
∴VT/Vsat =R1/Rf =R1/KR1 =1/K
Since the saturation voltage is much high compared to VT
∴VT/Vsat <1
∴1/K<1
∴K>1
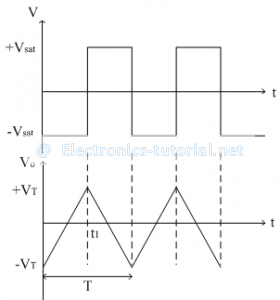
The following figure shows the signals at the output of the two op-amps.
Let us assume that the output of Schmitt trigger is in negative saturation (i.e. V= -Vsat). This negative dc signal is applied as an input to the inverting integrator. As seen in previous sections, the output of integrator for a step input is a ramp signal. Thus for negative input, the integrator produces a positive ramp signal as shown in the waveforms.
The output of the integrator (ramp signal) controlled by the triggering point VT. When the voltage across capacitor is crossing the threshold point +VT, the output of the Schmitt trigger is changed to +Vsat.
The output of an integrator is
Vo=-1/RC ∫(-Vsat )dt – VT
∴Vo=Vsat/RC(t) – VT
This positive voltage is again applied as an input to the integrator which produces a negative ramp signal as shown. When the negative threshold, -VT is crossed the Schmitt trigger is again changing its output to –Vsat.
The output of an integrator is
Vo=-1/RC ∫(+Vsat )dt+ VT
∴Vo=-Vsat/RC (t)+ VT
This cycle is repeated continuously so we get two waveforms (functions) square wave and triangular wave.